8.制約論理
トレースを追いながら制約論理プログラミングを習得しましょう。
各プログラムはインストールディレクトリの sample/clpに格納されていますので、Eclipseのプロジェクトにファイルをコピペして 実際にトレースをとりながら動かしてみましょう。
【つるかめ算】
つるかめ算は、つるとかめのように異なる足の数を持つ動物の個体数(頭数)の合計と足の数の合計が分かっているときに、 それぞれの個体数を求める算術です。
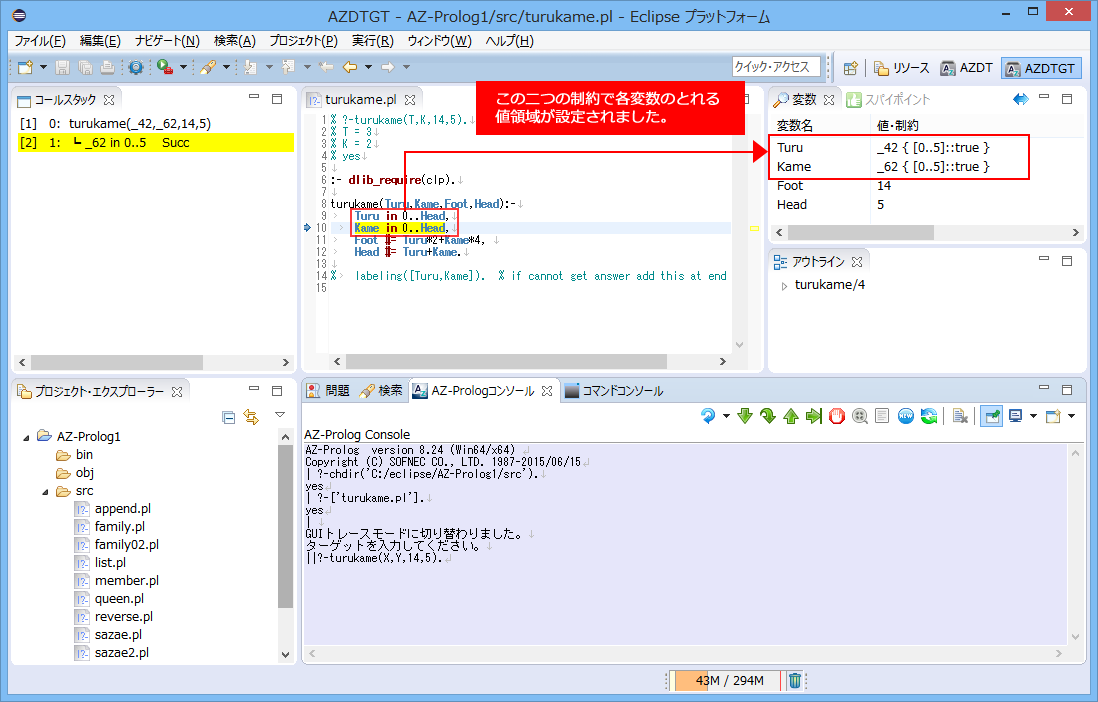
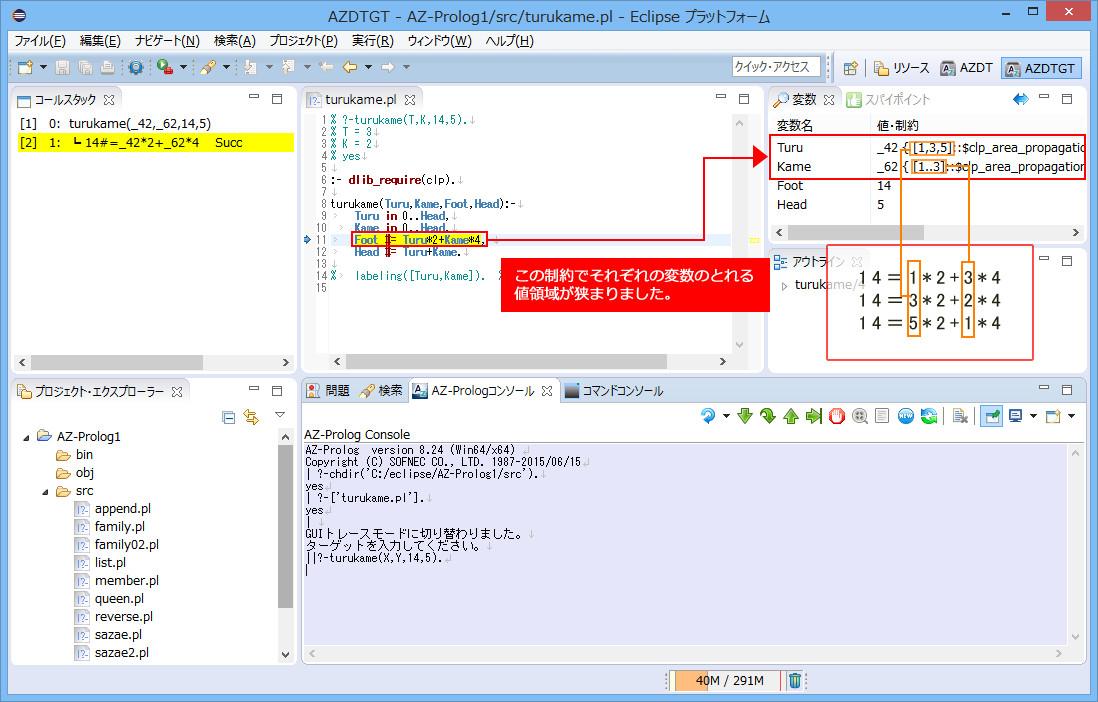
これを制約論理でプログラミングし、トレースを通じて変数の制約が絞られていく過程を見ながら、理解しましょう。
まず、プログラムの考え方を説明します。
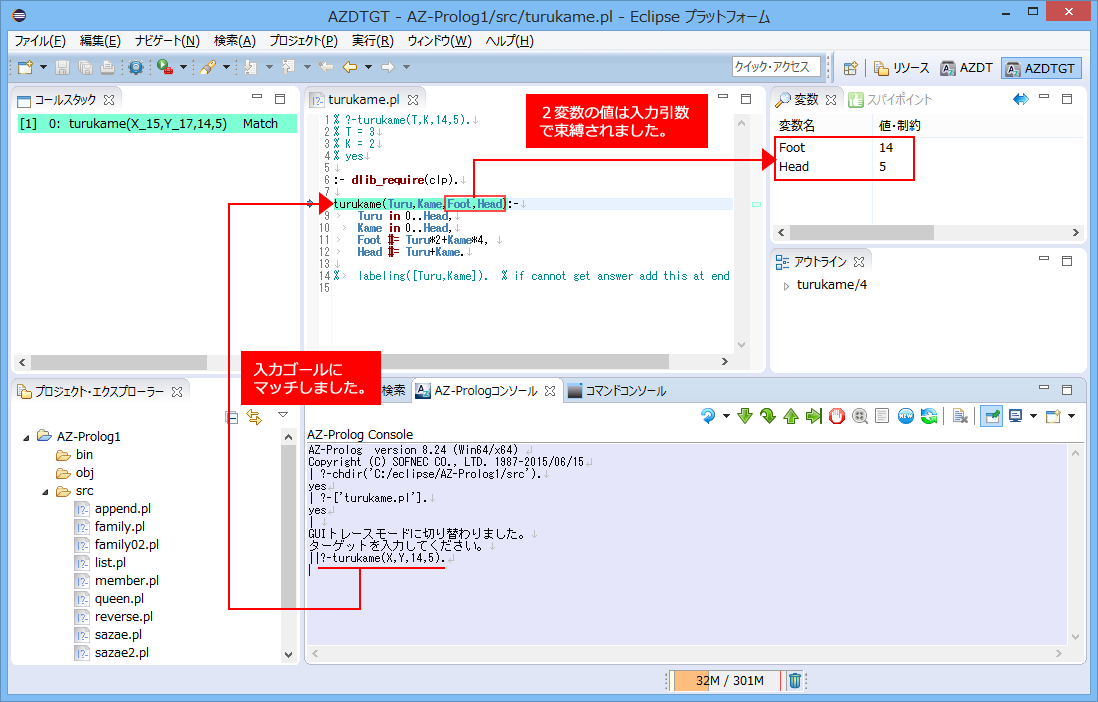
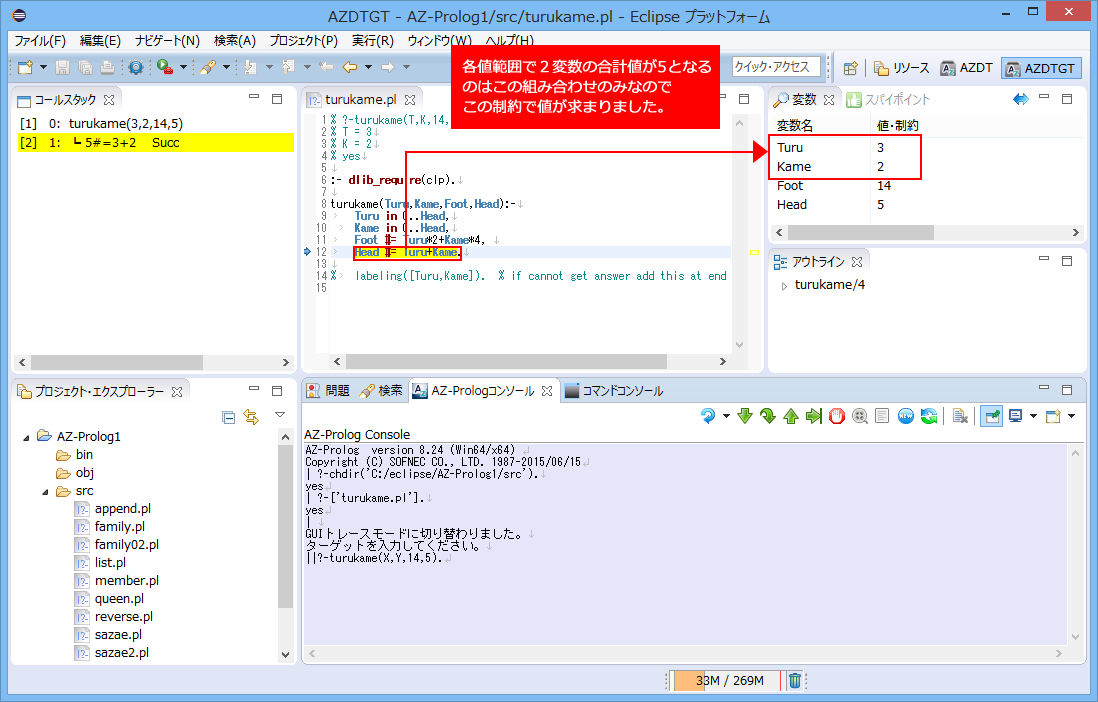
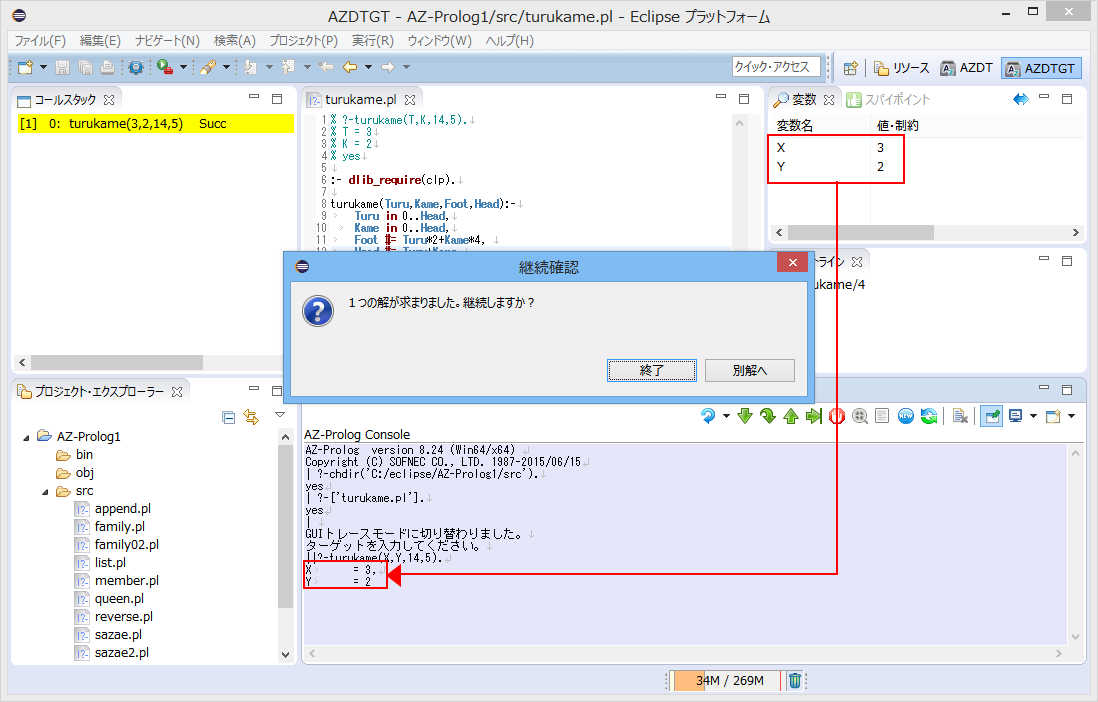
足の数(Foot)と頭の数(Head)を入力引数として渡し、Turuの数とKameの数を出力引数とする仕様にしてあります。
turukame(Turu,Kame,Foot,Head):-
Turu in 0..Head, %つるの数は最小0。負数を認めないのもつるかめ算
Kame in 0..Head, %つるの数の最大は(かめが0匹として)頭の総数(Head)匹。Headは正の整数でなければならない
%同様にかめの数も,0からHead匹。この二つがつるとかめの値領域となる
Foot #= Turu*2+Kame*4, %足の総数(Foot)は、つるの足は2本でかめの足は4本なので、これに各々の匹数を掛けたもの
Head #= Turu+Kame. %頭の総数(Head)は、つるとかめの匹数を足したもの
例では、足の数が14、頭の数が5でトレースを取っています。
【4×4数独】
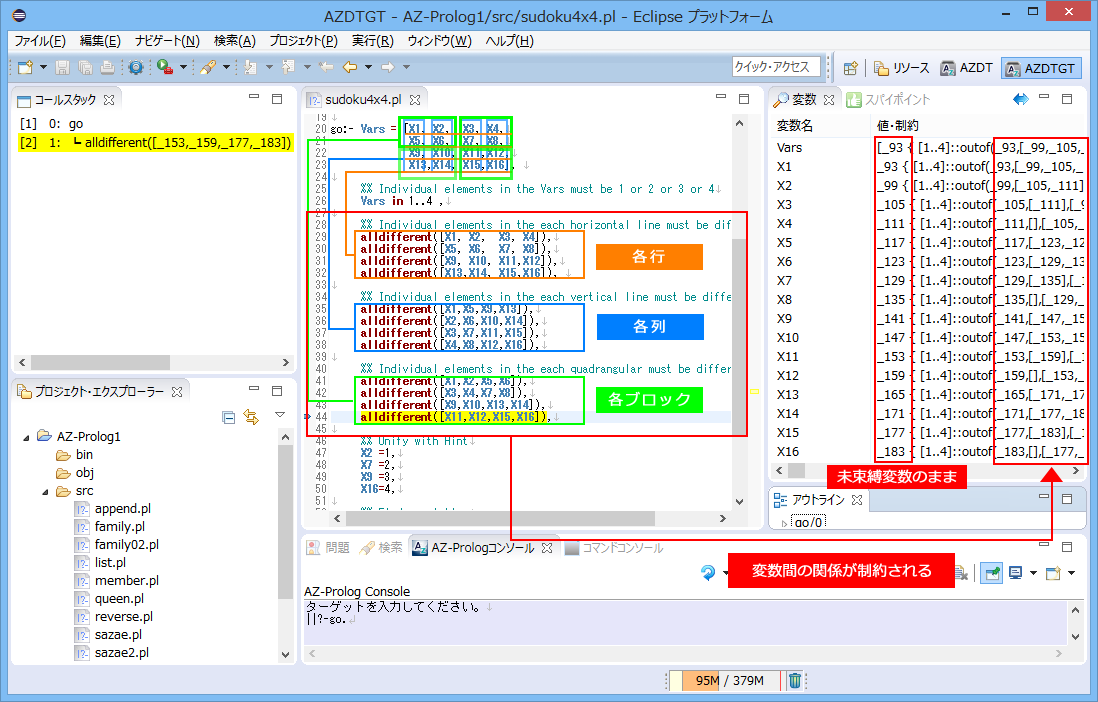
数独とは正方形の枠内の空いているマスに数字を埋めるパズルで、数字は各列(縦)/各行(横)/各ブロック内のいずれにも同じ数字が 複数含まれないように並べるのがルールです。
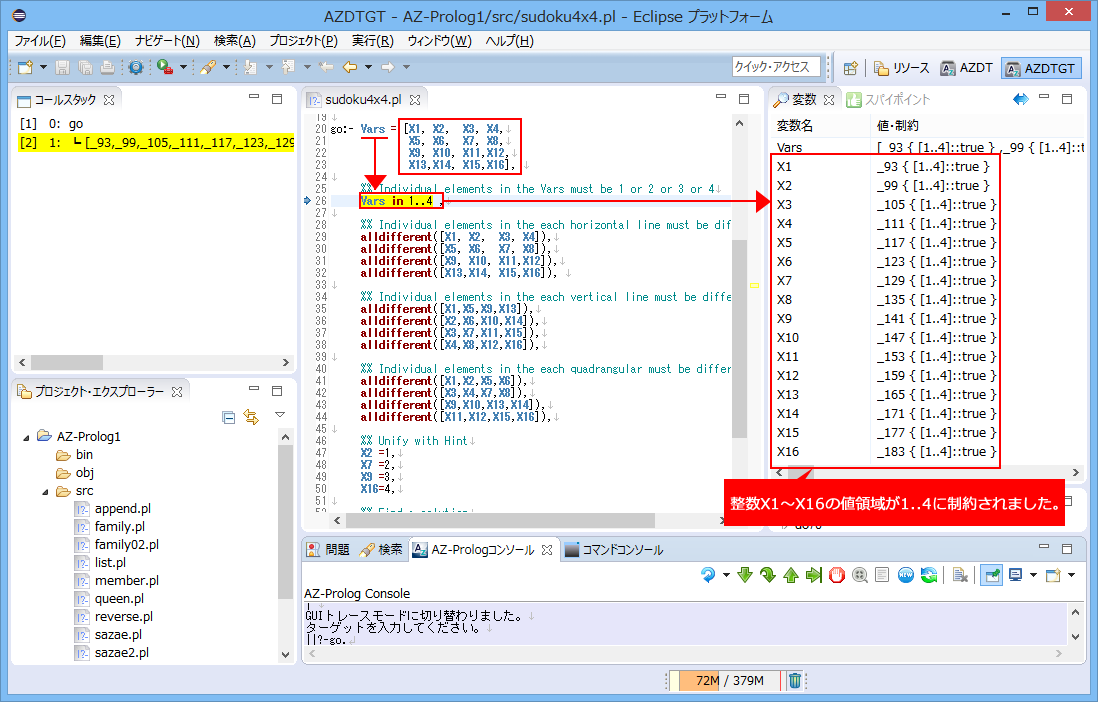
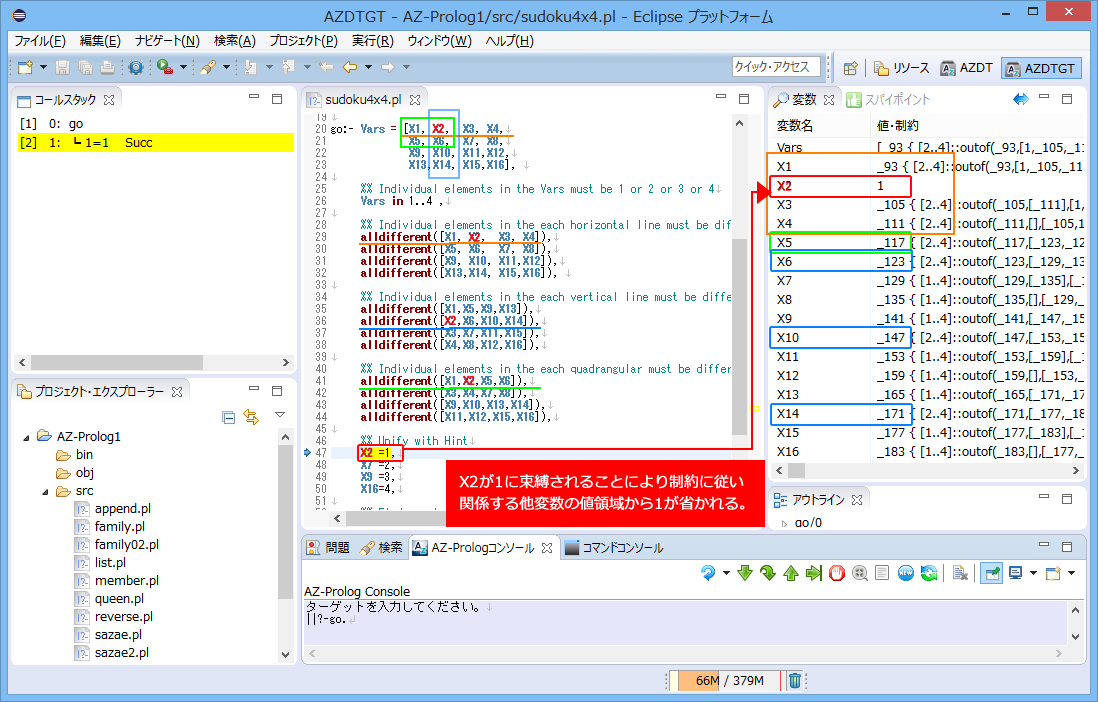
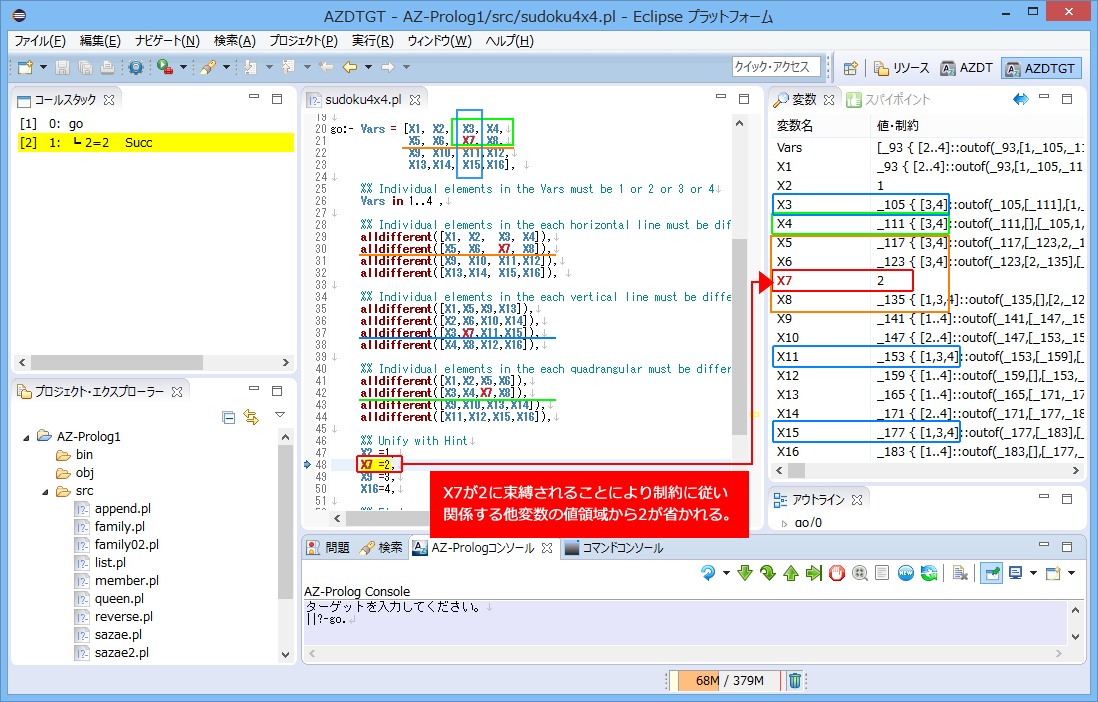
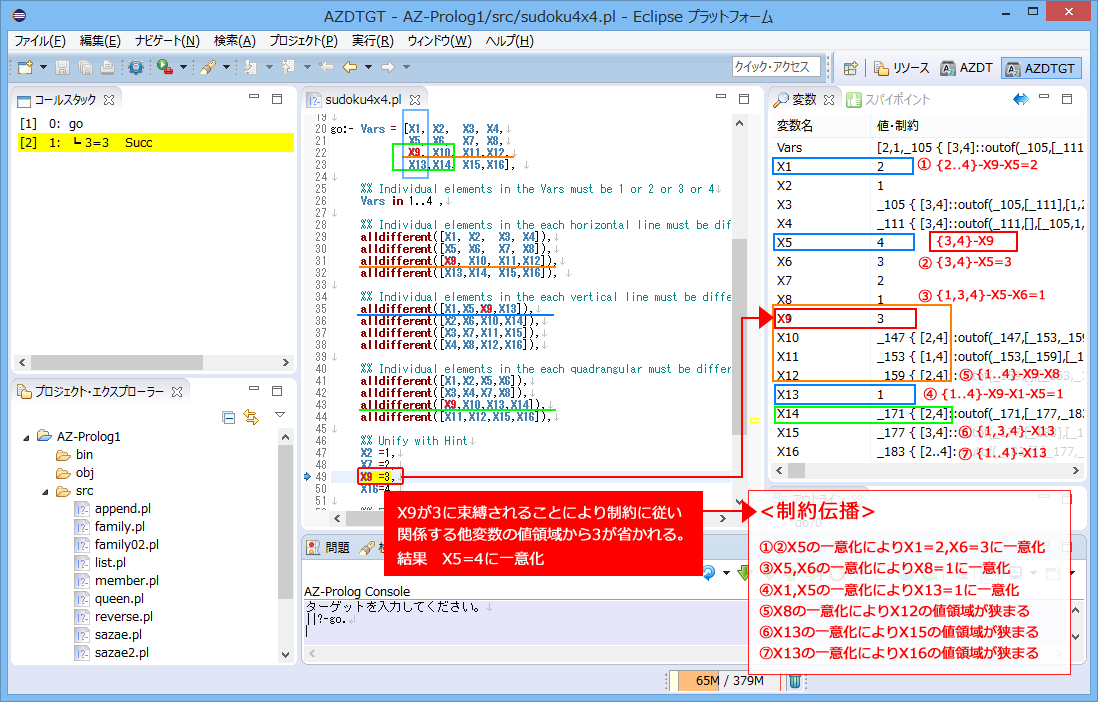
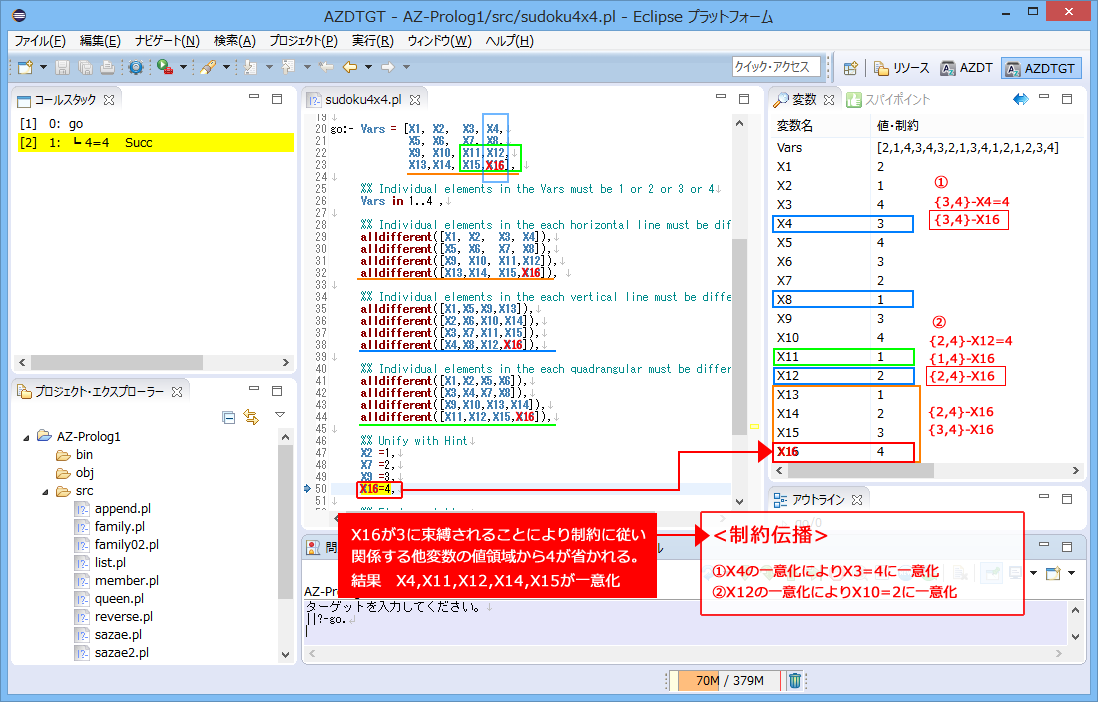
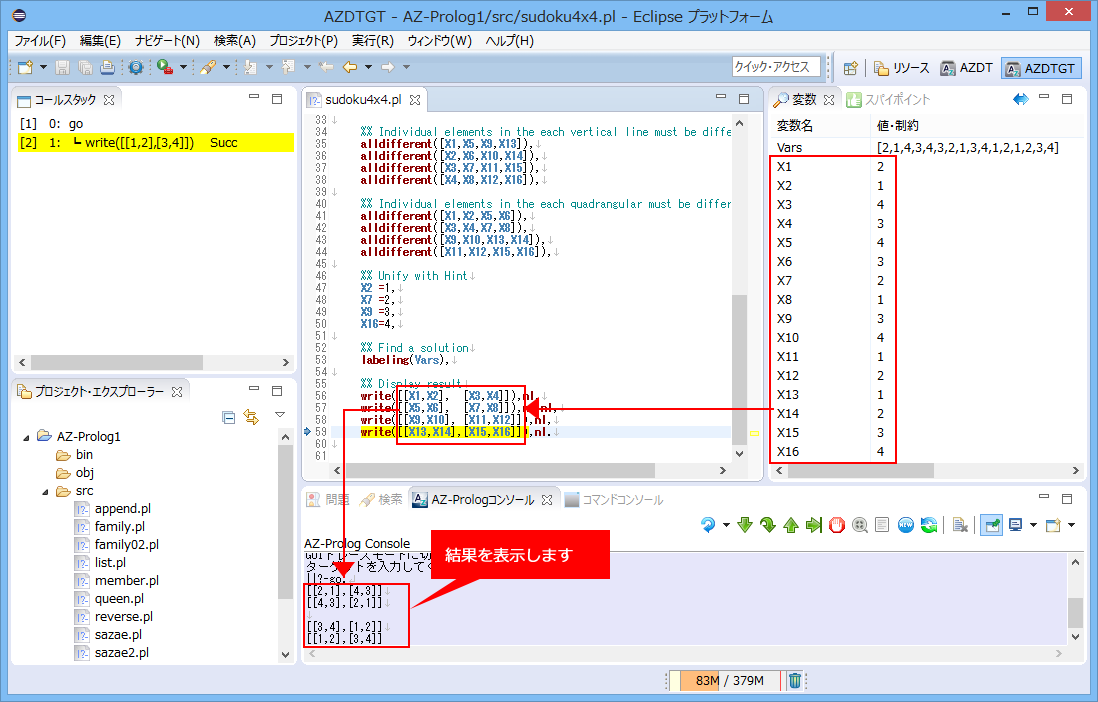
ここでは、説明を簡単にするため、4X4マス(2X2の4ブロック)からなる数独のトレースを追ってプログラムの考え方を理解しましょう。
ヒントとして、4つのマスの値が示されているとします。
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
プログラムを起動します。各マスは変数で、全体はそのリストで表現します。